利用贝叶斯网络预测医院服务患者数量译文精选-新利18国际娱乐

译者 | 朱先忠

审校 | 重楼

驾驭复杂性：预测医疗保健中的患者数量

在医疗保健领域，准确预测即将到来的患者数量不仅对手术成功至关重要，也是一个非常棘手的问题。原因很简单：需要考虑的依赖性因素太多了——患者的严重程度和特殊要求、管理需求、检查室限制、员工请病假、严重的暴风雪等等。更糟糕的是，意外情况可能会对日程安排和资源分配产生连锁影响，甚至可能与最高质量的Excel项目预测结果产生矛盾。

从数据的角度来看，这些挑战真的很有趣，因为它们极其复杂，足够你考虑一段时间的。但是，即使是轻微的改进也可能带来重大的胜利（例如，提高患者吞吐量、缩短等待时间、让医疗保健提供者更快乐、降低成本等）。

另一种预测方法：贝叶斯模型

那么，还有什么替代方案呢？Epic为我们提供了大量数据，包括患者何时赴约的实际记录。在已知历史“显示”和“未显示”的情况下，我们可以在监督学习的空间中操作，贝叶斯网络（BN：Bayesian Networks）提供了很好的概率图形模型来预测未来的访问概率。

虽然生活中的大多数决定都可以通过一个输入来决定（例如，考虑“我应该带雨衣吗？”。假设外面下雨，那么这个决定应该是“是”），但贝叶斯网络可以很容易地处理更复杂的决策——涉及多个输入的决策（例如，天气潮湿，步行仅3分钟，你的雨衣在另一层楼，你的朋友可能有伞，等等），具有不同的概率结果和依赖性。在这篇文章中，我将在Python语言环境中构造一个超简单的贝叶斯网络，它可以根据症状、癌症分期和治疗目标这三个因素的已知概率，输出患者在2个月内到达的概率得分。

理解贝叶斯网络

贝叶斯网络的核心是使用有向无环图（DAG）的联合概率分布的图形表示。DAG中的节点表示随机变量，有向边表示这些变量之间的因果关系或条件依赖关系。正如所有数据科学项目一样，在一开始就花大量时间与利益相关者协商，以正确映射决策中涉及的工作流程（例如变量），这对于高质量的预测结果是至关重要的。

因此，我将发明一个场景，让我们与乳腺肿瘤合作伙伴会面，由他们来解释三个变量——患者症状、癌症分期和当前治疗目标，对于确定患者是否需要在2个月内预约至关重要。

（事实上，影响未来患者数量的因素不下几十个，其中一些是单一或多重依赖性的，另一些则是完全独立但仍有影响的）。

现在，假设我们同意如下工作流程：阶段取决于他们的症状，但治疗类型与症状无关，也影响到2个月内的预约。

基于此，我们将从我们的数据源（对我们来说是Epic）中获取这些变量的数据，该数据源将再次包含我们的分数节点（Appointment_2months）的已知值，标记为“是”或“否”。这种数据整理是一个重要部分；你需要根据这些变量在2个月前表明的情况，正确地捕捉2个月内真正到达患者的病例。

# 安装包
import pandas as pd # 用于数据处理 
import networkx as nx # 用于绘图
import matplotlib.pyplot as plt # 用于绘图

!pip install pybbn
# 用于创建贝叶斯置信网络（BBN）
from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.jointree import EvidenceBuilder
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.pptc.inferencecontroller import InferenceController

# 通过手动键入概率创建节点
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), [0.30658, 0.69342])
Stage = BbnNode(Variable(1, 'Stage', ['Stage_III_IV', 'Stage_I_II']), [0.92827, 0.07173, 
 0.55760, 0.44240])
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), [0.58660, 0.24040, 0.17300])
Appointment_2weeks = BbnNode(Variable(3, 'Appointment_2weeks', ['No', 'Yes']), [0.92314, 0.07686, 
 0.89072, 0.10928, 
 0.76008, 0.23992, 
 0.64250, 0.35750, 
 0.49168, 0.50832, 
 0.32182, 0.67818])

上面代码中，让我们手动输入每个变量（节点）中对应级别的一些概率值。注意，这些概率值没有被猜测，甚至会是最好的猜测结果。不过，在实践应用中，您还将再次根据现有数据来计算对应的频率。

让我们以症状（symptom）变量为例。我会得到它们的2级频率值：大约31%是非恶性的，69%是恶性的，请参考下图：

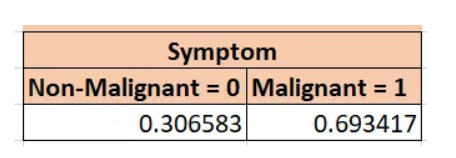
然后，我们考虑下一个变量Stage，并使用Symptom进行交叉表计算，以获得这些频率。我们这样做是因为阶段（Stage）取决于症状（Symptom），因为它们每个变量都对应两个场景，所以它们实际上存在4个概率结果。

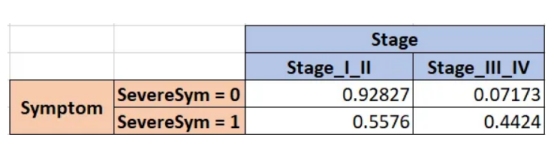
依此类推，直到定义了父子对之间的所有交叉表。

现在，大多数贝叶斯网络包括许多父子关系，因此计算概率可能会变得乏味（而且非常容易出错），下面的函数可以用来计算与0、1或2个父节点对应的任何子节点的概率矩阵。虽然医学洞见不能也不应该被自动化处理，但数据准备部分的工作完全可以也应该通过自动化的方式来实现。

# 此函数有助于计算进入BBN的概率分布（注意，最多可以处理2个父节点）
def probs(data, child, parent1=None, parent2=None):
 if parent1==None:
 # 计算概率
 prob=pd.crosstab(data[child], 'Empty', margins=False, normalize='columns').sort_index().to_numpy().reshape(-1).tolist()
 elif parent1!=None:
 # 检查子节点是否有1个父节点或2个父节点
 if parent2==None:
 # 计算概率
 prob=pd.crosstab(data[parent1],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
 else: 
 # 计算概率
 prob=pd.crosstab([data[parent1],data[parent2]],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
 else: print("Error in Probability Frequency Calculations")
 return prob

接下来，我们创建实际的贝叶斯网络节点和网络本身：

# 通过使用我们早期的函数自动计算概率来创建节点
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), probs(df, child='SymptomCat'))
Stage = BbnNode(Variable(1, 'Stage', ['Stage_I_II', 'Stage_III_IV']), probs(df, child='StagingCat', parent1='SymptomCat'))
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), probs(df, child='TreatmentTypeCat'))
Appointment_2months = BbnNode(Variable(3, 'Appointment_2months', ['No', 'Yes']), probs(df, child='Appointment_2months', parent1='StagingCat', parent2='TreatmentTypeCat'))

# 创建贝叶斯网络
bbn = Bbn() \
 .add_node(Symptom) \
 .add_node(Stage) \
 .add_node(TreatmentTypeCat) \
 .add_node(Appointment_2months) \
 .add_edge(Edge(Symptom, Stage, EdgeType.DIRECTED)) \
 .add_edge(Edge(Stage, Appointment_2months, EdgeType.DIRECTED)) \
 .add_edge(Edge(TreatmentTypeCat, Appointment_2months, EdgeType.DIRECTED))

# 将BBN转换为连接树
join_tree = InferenceController.apply(bbn)

现在，我们准备好了一切。接下来，让我们通过贝叶斯网络运行一些假设，并给出评估输出。

评估贝叶斯网络输出

首先，让我们看看每个节点的概率，而不需要具体声明任何条件。

# 定义打印边际概率的函数
#每个节点的概率
def print_probs():
 for node in join_tree.get_bbn_nodes():
 potential = join_tree.get_bbn_potential(node)
 print("Node:", node)
 print("Values:")
 print(potential)
 print('----------------')

# 使用以上函数打印边际概率
print_probs()
输出结果如下：
Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|0.67124
1=Stage_III_IV|0.32876
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.69342
0=Malignant|0.30658
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.58660
2=Treatment|0.17300
2=Therapy|0.24040
----------------
Node: 3|Appointment_2weeks|No,Yes
Values:
3=No|0.77655
3=Yes|0.22345
----------------

上述情况表明，该数据集中的所有患者都有67%的概率为Stage_I_II，69%的概率为非恶性（Non-Malignant），58%的概率需要辅助/新辅助（Adjuvant/Neoadjuvant）治疗，其中只有22%的患者需要在2个月后预约。

显然，我们可以很容易地从没有贝叶斯网络的简单频率表中得到这一点。

但现在，让我们问一个更有条件的问题：考虑到患者患有阶段=Stage_I_II和TreatmentTypeCat=Therapy，患者在2个月内需要护理的可能性有多大。此外，考虑到医疗保健提供者对他们的症状一无所知（也许他们还没有见过病人）。

我们将在节点中运行我们所知道的正确内容：

# 添加已发生事件的证据，以便重新计算概率分布
def evidence(ev, nod, cat, val):
 ev = EvidenceBuilder() \
 .with_node(join_tree.get_bbn_node_by_name(nod)) \
 .with_evidence(cat, val) \
 .build()
 join_tree.set_observation(ev)

# 添加更多证据
evidence('ev1', 'Stage', 'Stage_I_II', 1.0)
evidence('ev2', 'TreatmentTypeCat', 'Therapy', 1.0)
# 打印边际概率
print_probs()

上述代码的执行将返回如下内容：

Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|1.00000
1=Stage_III_IV|0.00000
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.57602
0=Malignant|0.42398
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.00000
2=Treatment|0.00000
2=Therapy|1.00000
----------------
Node: 3|Appointment_2months|No,Yes
Values:
3=No|0.89072
3=Yes|0.10928
----------------

上面结果显示，这个病人在两个月内到达的几率只有11%。我们可以询问我们变量的已知或未知特征的任何排列，以预测患者在2个月内到达的概率。可以利用进一步的算法和函数来收集许多患者或患者组的概率，或优化这些概率。

关于质量输入变量重要性的说明

Python代码编写是一回事，但贝叶斯网络在提供可靠的未来就诊估计方面的真正成功在很大程度上取决于患者护理工作流程的准确映射。所有这些需要时间、谈话和白板——而不是仅仅的编码工作。这样的信息取得甚至可能需要几次数据挖掘，并与客户重新接触，以进行压力测试假设：“我们之前说过，护士导航仪总是在报告症状不佳后给患者打电话，但这种情况只发生了10%。下一次与患者交谈是与他们的医疗服务提供者进行的。”。

在类似的情况下，表现相似的患者通常需要类似的服务，并以类似的节奏进入。这些输入的排列，其特征可以从临床到管理，最终对应于服务需求的某种确定性路径。但是，时间预测越复杂或越远，就越需要更具体、更复杂的具有高质量输入的贝叶斯网络。

原因如下：

精确表示：贝叶斯网络的结构必须反映变量之间的实际关系。选择不当的变量或误解的依赖关系可能导致不准确的预测和见解。
有效推理：高质量的输入变量增强了模型执行概率推理的能力。当变量根据其条件依赖性准确连接时，网络可以提供更可靠的见解。
降低复杂性：包含不相关或冗余的变量会使模型不必要地复杂化，并增加计算需求。高质量的投入使网络更加高效。

译者介绍

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。

原文标题：Using Bayesian Networks to forecast ancillary service volume in hospitals，作者：Gabe Verzino

利用贝叶斯网络预测医院服务患者数量译文精选

驾驭复杂性：预测医疗保健中的患者数量

另一种预测方法：贝叶斯模型

理解贝叶斯网络

评估贝叶斯网络输出

关于质量输入变量重要性的说明

译者介绍

评论

热门资讯

传感学人

相关阅读

无以叠加

NLP问题实战：基于LSTM（RNN）和Transformer模型译文精选

策略梯度强化学习算法实现A/B优化译文

什么是计算机网络？

CODESYS变量类型的范围和所占内存大小

振弦式应变计：轻松掌握应变量的神奇测量技巧

工业照明：安森美将推出更节能更安全的智联照明创新方案

意法半导体新型软件工具可实时显示应用程序运行时的变量

解读边缘智能（3）：边缘节点通信

无线传感器的基本网络架构及其应用

传感学人

点击进入下一篇

利用贝叶斯网络预测医院服务患者数量 译文 精选

驾驭复杂性：预测医疗保健中的患者数量

另一种预测方法：贝叶斯模型

理解贝叶斯网络

评估贝叶斯网络输出

关于质量输入变量重要性的说明

译者介绍

评论

热门资讯

传感学人

相关阅读

无以叠加

NLP问题实战：基于LSTM（RNN）和Transformer模型 译文 精选

策略梯度强化学习算法实现A/B优化​ 译文

什么是计算机网络？

CODESYS变量类型的范围和所占内存大小

振弦式应变计：轻松掌握应变量的神奇测量技巧

工业照明：安森美将推出更节能更安全的智联照明创新方案

意法半导体新型软件工具可实时显示应用程序运行时的变量

解读边缘智能（3）：边缘节点通信

无线传感器的基本网络架构及其应用

传感学人

点击进入下一篇

利用贝叶斯网络预测医院服务患者数量译文精选

NLP问题实战：基于LSTM（RNN）和Transformer模型译文精选

策略梯度强化学习算法实现A/B优化译文