译者 | 朱先忠
审校 | 孙淑娟
[提要]在本文中,我们将学习一种机器学习模型可伸缩超参数调整的新方法——Mango。
引言
模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。
优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的结果。在随机网格搜索中,通过仅在网格空间的随机点样本上训练模型来获得最佳超参数。
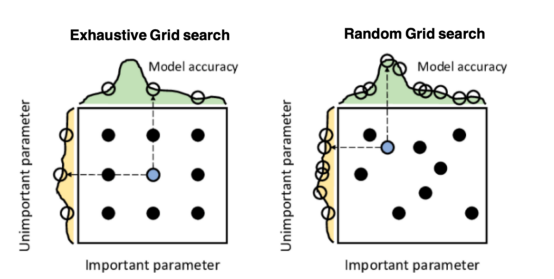
上图给出了两种网格搜索类型之间的比较。其中,九个点表示参数的选择,左侧和顶部的曲线表示作为每个搜索维度的函数的模型精度。该数据摘自Salgado Pilario等人发表在《IEEE工业电子学报》上的论文(68,6171–6180,2021)。
长期以来,两种网格搜索算法都被数据科学家广泛用于寻找最优模型超参数。然而,这些方法通常会找到损失函数远离全局最小值的模型超参数。
然而,到了2013年,这一历史发生了变化。这一年,James Bergstra和他的合作者发表了一篇论文,其中探索了贝叶斯优化技术,以便找到图像分类神经网络的最佳超参数,他们将结果与随机网格搜索的结果进行了比较。最后的结论是,贝叶斯方法优于随机网格搜索,请参考下图。
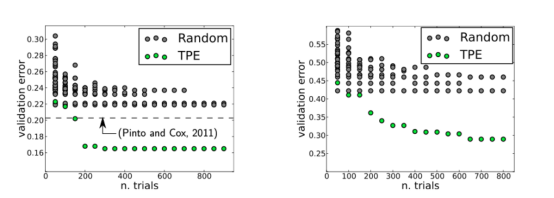
图中展示的是LFW数据集(左)和PubFig83数据集(右)上的验证错误。其中,TPE,即“Tree Parzen Estimator”,它是贝叶斯优化中使用的一种算法。该图摘自Bergstra等人发表在《机器学习研究学报》上的论文(28,115–123,2013)。
但是,为什么贝叶斯优化比任何网格搜索算法都好呢?因为这是一种引导方法,它对模型超参数进行智能搜索,而不是通过反复试验来找到它们。
在本文中,我们将细致剖析上述贝叶斯优化方法,并将通过一个名为Mango的相对较新的Python包来探索这种算法的一种实现版本。
贝叶斯优化
在解释Mango能够做什么之前,我们需要先来了解贝叶斯优化是如何工作的。当然,如果您对该算法已经非常理解,您可以跳过本节的阅读。
归纳来看,贝叶斯优化共有4个部分:
- 目标函数:这是您想要最小化或最大化的真实函数。例如,它可以是回归问题中的均方根误差(RMSE)或分类问题中的对数损失函数。在机器学习模型的优化中,目标函数依赖于模型超参数。这就是为什么目标函数也称为黑箱函数,因为其形状未知。
- 搜索域或搜索空间:这对应于每个模型超参数具有的可能取值。作为用户,您需要指定模型的搜索空间。例如,随机森林回归模型的搜索域可能是:
param_space = {'max_depth': range(3, 10),
'min_samples_split': range(20, 2000),
'min_samples_leaf': range(2, 20),
'max_features': ["sqrt", "log2", "auto"],
'n_estimators': range(100, 500)
}贝叶斯优化使用定义的搜索空间对目标函数中评估的点进行采样。
- 代理模型:评估目标函数非常昂贵,因此在实践中,我们只在少数地方知道目标函数的真实值。然而,我们需要知道其他地方的值。这正是代理模型出场的时候,代理模型是建模目标函数的工具。代理模型的常见选择是所谓的高斯过程(GP:Gaussian Processes),因为它能够提供不确定性估计。
在贝叶斯优化开始时,代理模型从先验函数开始,该先验函数沿搜索空间以均匀的不确定性分布:
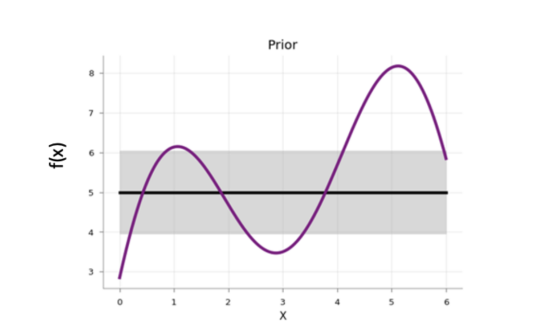
图中展示了代理模型的先验函数取值情况。其中,阴影区域代表不确定性,而黑线代表其平均值,紫色线表示一维目标函数。此图片摘自2020年一篇探索贝叶斯优化的博客文章,作者是Aporv Agnihotri和Nipun Batra。
每次在目标函数中评估搜索空间中的样本点时,该点处代理模型的不确定性变为零。经过多次迭代后,代理模型将类似于目标函数:
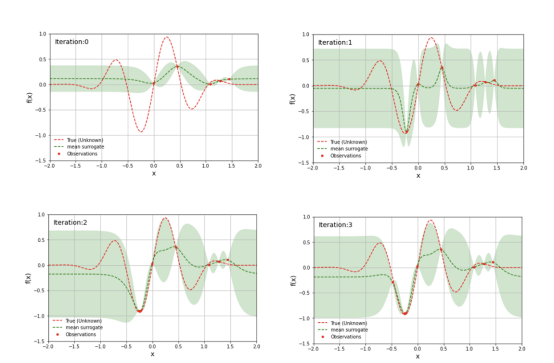
简单一维目标函数的代理模型
然而,贝叶斯优化的目标不是对目标函数建模,而是以尽可能少的迭代次数找到最佳模型超参数。为此,需要使用一种采集(acquisition)函数。
- 采集函数:该函数是在贝叶斯优化中引入的,用于指导搜索。采集函数用于评估是否需要基于当前代理模型对点进行评估。一个简单的采集函数是对代理函数的平均值最大化的点进行采样。
贝叶斯优化代码的步骤是:
选择用于建模目标函数的代理模型,并定义其先验for i = 1, 2,..., 迭代次数:
- 给定目标中的一组评估,使用贝叶斯方法以获得后验。
- 使用一个采集函数(这是一个后验函数)来决定下一个采样点。
- 将新采样的数据添加到观测集。
下图显示了简单一维函数的贝叶斯优化:
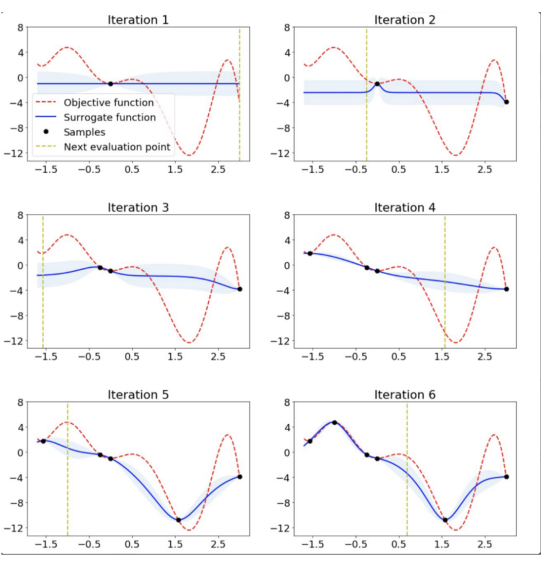
上图给出了一维函数的贝叶斯优化。图片摘自ARM research的博客文章《AutoML的可伸缩超参数调整》。
其实,有不少Python软件包都在幕后使用贝叶斯优化来获得机器学习模型的最佳超参数。例如:Hyperopt;Optuna;Bayesian optimization;Scikit-optimize (skopt);GPyOpt;pyGPGO和Mango,等等。这里仅列举了其中的一部分。
现在,让我们正式开始Mango的探讨。
Mango:为什么这么特别?
近年来,各行业数据量大幅增长。这对数据科学家来说是一个挑战,这需要他们的机器学习管道具有可扩展性。分布式计算可能会解决这个问题。
分布式计算指的是一组计算机,它们在相互通信的同时执行共同的任务;这与并行计算不同。在并行计算中,任务被划分为多个子任务,这些子任务被分配给同一计算机系统上的不同处理器。
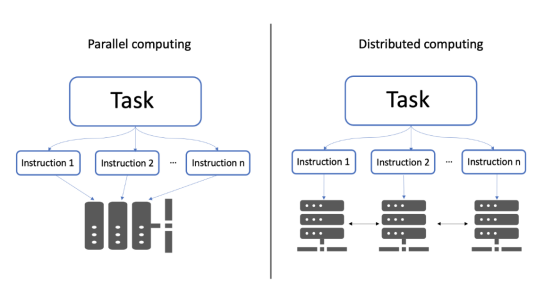
并行计算与分布式计算架构示意图。
尽管有相当多的Python库使用贝叶斯优化来优化模型超参数,但它们都不支持任何分布式计算框架上的调度。Mango开发者的动机之一是,创建一种能够在分布式计算环境中工作的优化算法,同时保持贝叶斯优化的能力。
Mango体系结构的秘密是什么?使其在分布式计算环境中工作良好?Mango采用模块化设计构建,其中优化器与调度器是解耦设计的。这种设计允许轻松扩展使用大量数据的机器学习管道。然而,这种架构在优化方法中面临挑战,因为传统的贝叶斯优化算法是连续的;这意味着,采集函数仅提供单个下一个点来评估搜索。
Mango使用两种方法来并行化贝叶斯优化:一种是称为批高斯过程的方法bandits,另一种方法是k-means聚类。在本博客中,我们将不解释批量高斯过程。
关于聚类方法,IBM的一组研究人员于2018年提出了使用k-means聚类来横向扩展贝叶斯优化过程(有关技术细节,请参阅论文https://arxiv.org/pdf/1806.01159.pdf)。该方法包括从搜索域中采样的聚类点,这些点在采集函数中生成高值(参见下图)。在开始时,这些聚类在参数搜索空间中彼此远离。当发现代理函数中的最佳区域时,参数空间中的距离减小。k-means聚类方法水平扩展优化,因为每个聚类用于作为单独的过程运行贝叶斯优化。这种并行化导致更快地找到最优模型超参数。

Mango使用聚类方法来扩展贝叶斯优化方法。采集函数上的彩色区域是由搜索空间中具有高采集函数值的采样点构建的聚类。开始时,聚类彼此分离,但由于代理函数与目标相似,它们的距离缩短。(图片摘自ARM research的博客文章《AutoML的可伸缩超参数调整》)
除了能够处理分布式计算框架之外,Mango还与Scikit-learn API兼容。这意味着,您可以将超参数搜索空间定义为Python字典,其中的键是模型的参数名,每个项都可以用scipy.stats中实现的70多个分布中的任何一个来定义。所有这些独特的特性使Mango成为希望大规模利用数据驱动解决方案的数据科学家的好选择。
简单示例
接下来,让我们通过一个实例展示Mango是如何在优化问题中工作的。首先,您需要创建一个Python环境,然后通过以下命令安装Mango:
pip install arm-mango
在本例中,我们使用可直接从Scikit-learn加载的加州住房数据集(有关此链接的更多信息请参考https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html):
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
import time
from mango import Tuner
housing = fetch_california_housing()
# 从输入数据创建数据帧
# 注:目标的每个值对应于以100000为单位的平均房屋价值
features = pd.DataFrame(housing.data, columns=housing.feature_names)
target = pd.Series(housing.target, name=housing.target_names[0])
该数据集共包含20640个样本。每个样本包括房屋年龄、平均卧室数量等8个特征。此外,加州住房数据集还包括每个样本的房价,单位为100000。房价分布如下图所示:
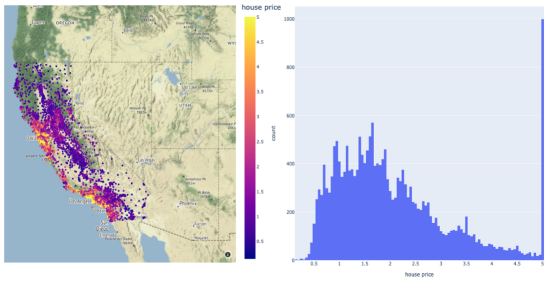
在图示的左面板中,显示了加利福尼亚数据集中房价的空间分布。右边给出的是相应于同一变量的直方图。
请注意,房价的分布有点偏左。这意味着,在目标中需要一些预处理。例如,我们可以通过Log或Box-Cox变换将目标的分布转换为正态形状。由于目标方差的减小,这种预处理可以提高模型的预测性能。我们将在超参数优化和建模期间执行此步骤。现在,让我们将数据集拆分成训练集、验证集和测试集三部分:
# 将数据集拆分成训练集、验证集和测试集
x_train, x_test, y_train, y_test = train_test_split(features, target, test_size=0.2, random_state=42)
x_train, x_validation, y_train, y_validation = train_test_split(x_train, y_train, test_size=0.2, random_state=42)
到目前,我们已经准备好使用Mango来优化机器学习模型。首先,我们定义Mango从中获取值的搜索空间。在本例中,我们使用了一种称为“极端随机树(Extreme Randomized Trees)”的算法,这是一种与随机森林非常相似的集成方法,不同之处在于选择最佳分割的方式是随机的。该算法通常以偏差略微增加为代价来减少方差。
极端随机化树的搜索空间可以按如下方式定义:
# 第一步:定义算法的搜索空间(使用range而不是uniform函数来确保生成整数)
param_space = {'max_depth': range(3, 10),
'min_samples_split': range(int(0.01*features.shape[0]), int(0.1*features.shape[0])),
'min_samples_leaf': range(int(0.001*features.shape[0]), int(0.01*features.shape[0])),
'max_features': ["sqrt", "log2", "auto"]
}
定义参数空间后,我们再指定目标函数。在这里,我们使用上面创建的训练和验证数据集;但是,如果您想运行k倍交叉验证策略,则需要在目标函数中由您自己来实现它。
# 第二步:定义目标函数
# 如果要进行交叉验证,则在目标中定义交叉验证
#在这种情况下,我们使用类似于1倍交叉验证的方法。
def objective(list_parameters):
global x_train, y_train, x_validation, y_validation
results = []
for hyper_params in list_parameters:
model = ExtraTreesRegressor(**hyper_params)
model.fit(x_train, np.log1p(y_train))
prediction = model.predict(x_validation)
prediction = np.exp(prediction) - 1 # to get the real value not in log scale
error = np.sqrt(mean_squared_error(y_validation, prediction))
results.append(error)
return results
关于上述代码,有几点需要注意:
- 目标函数旨在找到使均方根误差(RMSE)最小化的最佳模型参数。
- 在Scikit-learn中,回归问题的极端随机化树的实现称为ExtraTreesRegressor。
- 请注意,训练集中的房价要经过对数变换。因此,验证集上的预测被转换回其原始规模。
优化模型超参数所需的最后一步是实例化类Tuner,它负责运行Mango:
#第三步:通过Tuner运行优化
start_time = time.time()
tuner = Tuner(param_space, objective, dict(num_iteration=40, initial_random=10)) #初始化Tuner
optimisation_results = tuner.minimize()
print(f'The optimisation in series takes {(time.time()-start_time)/60.} minutes.')
#检查结果
print('best parameters:', optimisation_results['best_params'])
print('best accuracy (RMSE):', optimisation_results['best_objective'])
# 使用测试集上的最佳超参数运行模型
best_model = ExtraTreesRegressor(n_jobs=-1, **optimisation_results['best_params'])
best_model.fit(x_train, np.log1p(y_train))
y_pred = np.exp(best_model.predict(x_test)) - 1 # 获取实际值
print('rmse on test:', np.sqrt(mean_squared_error(y_test, y_pred)))
上述代码在MacBook Pro(处理器为2.3 Ghz四核英特尔酷睿i7)上运行了4.2分钟。
最佳超参数和最佳RMSE分别为:
best parameters: {‘max_depth’: 9, ‘max_features’: ‘auto’, ‘min_samples_leaf’: 85, ‘min_samples_split’: 729}
best accuracy (RMSE): 0.7418871882901833当在具有最佳模型参数的训练集上训练模型时,测试集上的RMSE为:
rmse on test: 0.7395178741584788
免责声明:运行此代码时可能会得到不同的结果。
让我们简要回顾一下上面代码中使用的类Tuner。此类有许多配置参数,但在本例中,我们只尝试了其中两个:
- num_iteration:这些是Mango用于找到最佳值的迭代总数。
- initial_random:该变量设置测试的随机样本数。注意:Mango将所有随机样本一起返回。这非常有用,尤其是在优化需要并行运行的情况下。
注意:本博客中发布的示例仅使用了一个小数据集。然而,在许多实际应用程序中,您可能会处理需要并行实现Mango的大型数据文件。如果您转到我的GitHub源码仓库,您可以找到此处显示的完整代码以及大型数据文件的实现。
总之,Mango用途广泛。您可以在广泛的机器和深度学习模型中使用它,这些模型需要并行实现或分布式计算环境来优化其超参数。因此,我鼓励您访问Mango的GitHub存储库。在那里,您可以找到许多工程源码,展示Mango在不同计算环境中的使用。
总结
在本博客中,我们认识了Mango:一个Python库,用于进行大规模贝叶斯优化。此软件包将使您能够:
- 扩展模型超参数的优化,甚至可以在分布式计算框架上运行。
- 轻松将scikit-learn模型与Mango集成,生成强大的机器学习管道。
- 使用scipy.stats中实现的任何概率分布函数,用于声明你的搜索空间。
所有这些特性使Mango成为一个独特的扩展您的数据科学工具包的Python库。
译者介绍
朱先忠,51CTO社区编辑,51CTO专家博客、讲师,潍坊一所高校计算机教师,自由编程界老兵一枚。
原文标题:Mango: A new way to do Bayesian optimization in Python,作者:Carmen Adriana Martinez Barbosa
